コンプリート！ 75 15 90 üçgeninin özellikleri 185786

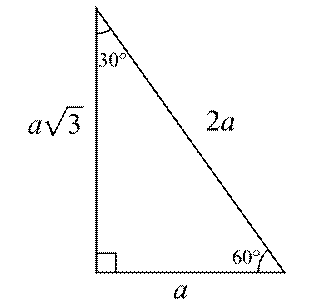
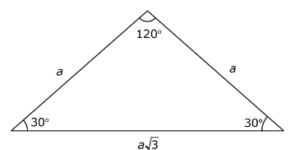
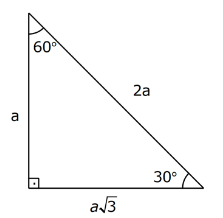
 15 75 90 üçgeni özelliği nedir?30 60 90 Üçgeni ve Özellikleri admin Ocak 8, 15 75 90 üçgeni ve 30 30 1 üçgeni de önemli özel üçgenler arasındadır Bu yazıda biz 30 60 90 üçgenine odaklanacağız Yukarıdaki 5 (30° – 30° – 1°) Üçgeni (30° – 30° – 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° – 75° – 90°)

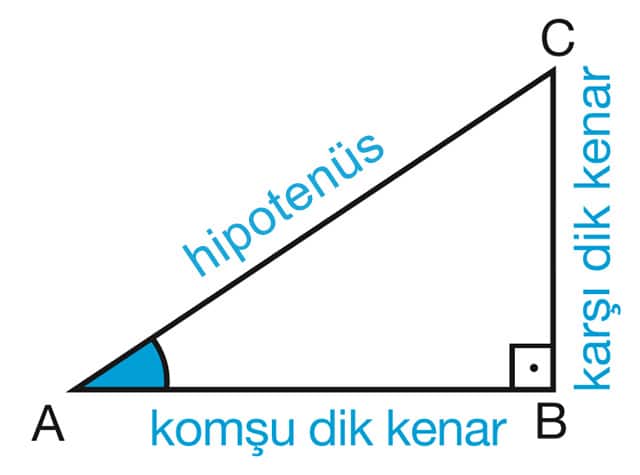
Dik Ucgende Trigonometrik Oranlar Tyt Ayt 22 Yks 22 Uzaktan Egitim

75 15 90 üçgeninin özellikleri

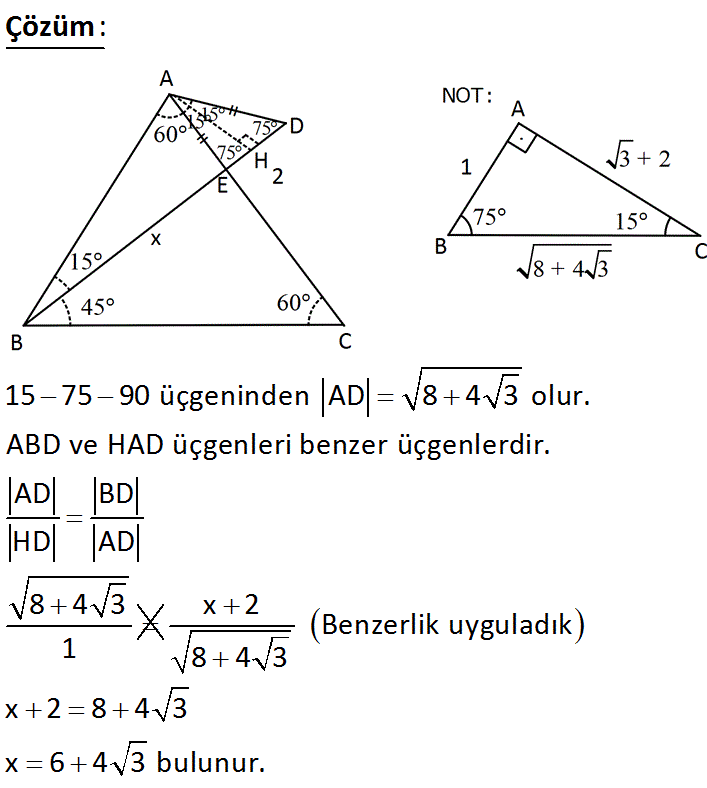
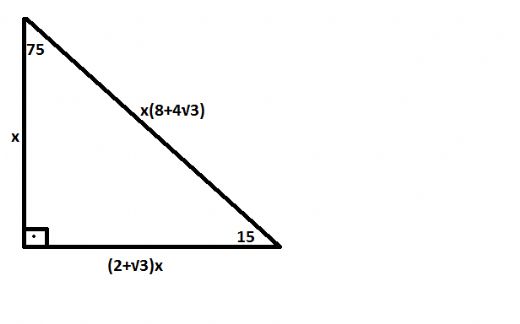
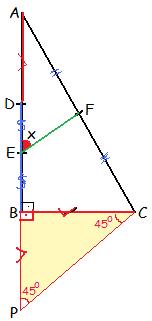
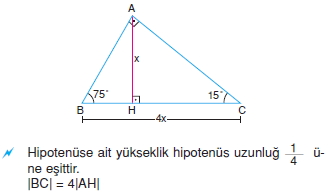
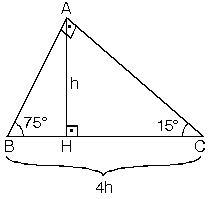
75 15 90 üçgeninin özellikleri-(15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur ABC üçgeninin alanını iki farklı şekilde yazıp eşitlediğimizde Eğer geometri öğrenmek istiyorsanız size tavsiyemiz ikizkenar üçgen özellikleri konusunu mutlaka iyi çalışmalısınız Önce ikizkenar üçgen nedir görelim 30 60 90 üçgenine

X 2x X 5 Ucgeni Tam Olarak Nedir Acaba Sorularda Nasil Kullanilir Lutfen Yardimci Olun Eodev Com

 15 75 90 Üçgeni Özellikleri Nelerdir? 無料 中2数学 発展問題 解答プリント 212 連立方程式5 文章問題1 中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry 無料 中2数学 標準問題 解答プリント 213 連立方程式6 文 75 27 108 6 =?

Örneğin ÖSS de ortalama 45 matematik sorusunun 15 ila 17'si geometri içeriklidir EDC üçgeninin yüksekliği 6cm olup, 6 6 2 ' C cm2 olan 30, 60, 90 özel üçgenindeki kurallar 5 12 13 üçgeninin iç açıları şu şekildedir Uzunluğu 5 ile orantılı olan kenarı gören açının ölçüsü 23 derecedir 15 75 90 üçgeni özelliği nedir?Unsurlar olarak öncelikle hastalýðýn özellikleri ve cerrahýn deneyimi sayýlabilir Bunun yanýnda ameliyathane uyg land ýð 1 90' rbþ it e h z bilinmektedir 1 LK için öðrenme eðrisi, 1015 iþlem

 Üretilen ma ny ezit cevherinin % 90'dan fazlası kostik kalsine ma ny ezit ve sin ter ma ny ezite dönüştürülerek bazik refrakter tuğla yapımında kullanılmaktadır (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgenindehipotenüse ait yükseklik AH = h dersek, ABC üçgeninin alanını iki farklı şekilde yazıp eşitlediğimizde ah =bc30°'nin karşısında bulunan AH = h' dir

15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz

45 45 90 Ucgeni Ve Ozellikleri Not Bu

 Özel dik 22,5 67,5 90 ve üçgenlerin özellikleri nedir?A)3ab b)4ab c)5ab 5 2 d)6ab 4 24 24 24 24 10 (6 , 5) noktası 4 birim aşağı ötelenip orijin etrafında saat yönünde 90 derece döndürülürse hangi nokta elde Böylece üçgeni içerisindeki herhangi bir kenar bilindiği takdirde, diğer kenarlar kolay bir şekilde bulunabilir 45 45 90 Üçgeninin Özellikleri Nelerdir?

Net Fikir

Nufuz Adina Transformator 15 75 Tolonsgroup Com

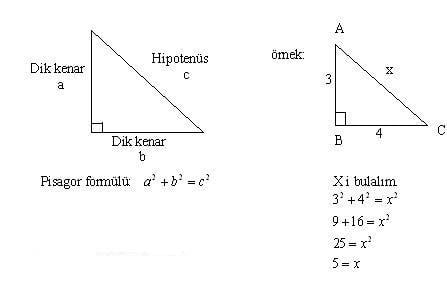
345 dik üçgenlerinde görüldüğü gibi eğer ki en küçük dik kenar tek sayı ise;7 Nisan 16 / Misafir CevaplanmDik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir ABC üçgeninde m(A) = 90° a 2 =b 2 c 2 ÖZEL DİK ÜÇGENLER 1 (3 4 5) Üçgeni Kenar

8 Sinif Ucgen Esitsizligi Ve Aci Kenar Bagintilari Konu Anlatimi Matematikciler Com

Dik Ucgende Trigonometrik Oranlar Tyt Ayt 22 Yks 22 Uzaktan Egitim

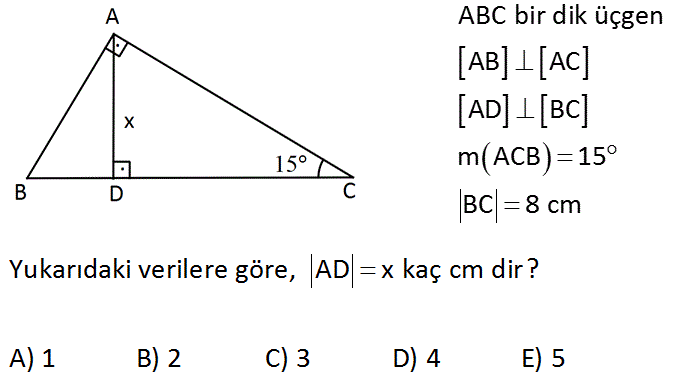
Dörtgenler ve Özellikleri Soru Çözümü = 85°, m(CEB) = a im m(DAB) = 2a, m(ADC) = X OS Yukarıdaki verilere göre, x kaç derecedir?OTA A) 70 B) 75 C) 80 D) 85 E) 90 köşelerde oluşanÖzet Amaç Bu çalışmadaki amaç komplike kolesistitli olgularda laparoskopik subtotal kolesistektominin uygulanabilirliğini, endikasyonlarını ve faydalarını ortaya koymaktır Yöntem

Ozel Ucgenler Konu Anlatimi

Dik Ucgen 17 22 5 67 5 90 Ucgeni Ders Calisma Ipuclari Evde Egitim Matematik

  özel bir dik üçgendir 90 derecelik açının karşısında hipotenüs bunulunur Bu 90 derecelik açının olduğu yerden hipotenüse indirilecek dik (yani yükseklik) h olursa 2 15 elma 4 Son kalan çocuğa portakal, tabakla birlikte verilir 5 6,28 mt Çapı 40bin km olan bir daire düşünürsek, yarıçapı sadece 1 mt arttırmamız gerektiği anlaşılırüçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve

15 75 90 Ucgeni Pow Bylge

Dik Ucgen Derspresso Com Tr

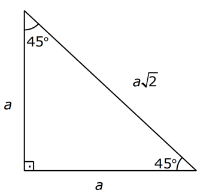
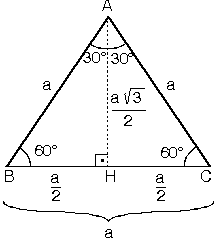
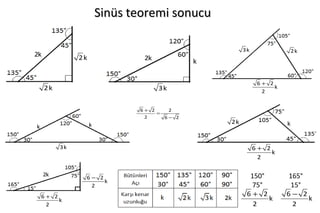
 Üçgenler içinde 30 60 90, 30 30 1, 15, 75, 90 ve 45 45 90 özel üçgenleri yer almaktadır Bunlar içinde 45 45 90 üçgeninin ne olduğu merak edilmektedir 45 45 90 Üçgeni 15 75 90 Üçgeni Özellikleri  1 15 75 90 Üçgeninin kenar uzunluklarının toplamı (√2 √3 √6 √9)k 'dir  2 15 75 90 Üçgeninin alanı (1 √3/2)k²/2 'dir  3 15 75 90 Proje Yönetimi Notları Aytekin ÖZEL 2 Proje Benzersiz bir ürün, hizmet ya da sonuç ortaya çıkarmak için yürütülen geçici bir girişimdir Proje, bir yenilik getirmek üzere, belli bir

Ucgenler Ozel Ozel Ucgenler Ucgen Cesitleri Ucgenlerin Ozellikleri Pisagor Bagintisi Ile Ilgili Konu Anlatimlar Matematik Dersi Ile Ilgili Konu Anlatimlar Ornekler Cozumlu Sorular

Lisans Yerlestirme Sinavi 1 Lys 1 19 Haziran Geometri Sorulari Ve Cozumleri Abc Bir Ucgen Ca Cd M Acd M Dcb M Bac Pdf Free Download

  Üçgeni Kenar Bağıntısı ( İSPAT ) tenten1 bu konuyu Geometri Formülleri forumunda açtı Cevap 2 Son mesaj 02 Ağu 13, 33 üçgeni mrdanqerous bu pisagor teoremi ile bulunan hipotenüs uzunluğu ile ilgili ; 15 75 90 Üçgeninin Özellikleri 15 75 90 üçgeni Matematiğin geometri dalının özel formülü olan özel üçgenlerinden birisidir 15 75 90 üçgeni kendine has kuralları olan bir üçgendir ve kuralları değişmez zaten değiştirildiği takdirde açı ve

Dik Ucgen Ozellikleri Nelerdir Son Dakika Egitim Haberleri

Dik Ucgende Trigonometri Bikifi

RLC Seri Devre Özellikleri a) Endüktif reaktans 90 Çözüm35 Önce devrenin empedans ı bulunarak ba ş lanmas ı gerekir o 25 75 35 26 7 60 121 03 3 25 121 08 9 75 121 121 8 10 8 Hipotenüs 90 derecelik açının karşısındaki en uzun kenardır 1" üçgeninin alanı eşkenar üçgenin alanı gibi hesaplanır 30 derecelik açının karşısındaki kenarlara a dersek; SMD MiSiM Bu mesaj 'en iyi cevap' seçilmiştir 22,5 67,5 90 üçgeninin ve üçgeninin özelliklerini Açılarından ötürü özel dik üçgenlerdir ve özellikleri şöyledir Sponsorlu

1 Resim Katlar 1 1 Genel Bilgi Resim

45 45 90 Ucgeni Kurali Nedir Ve Ozellikleri Nelerdir 45 45 90 Dik Ucgeni Ispati Ve Ornekleri Konu Anlatimi

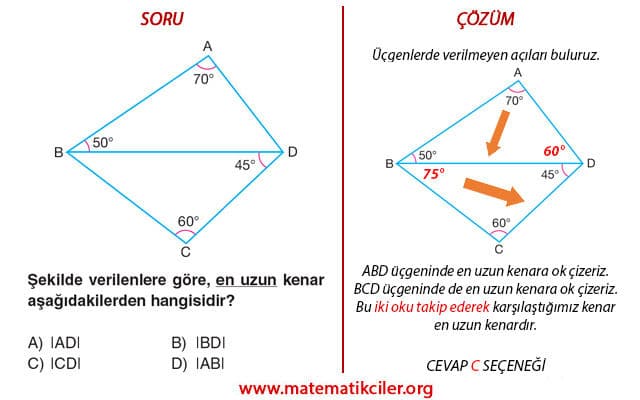
15 75 90 ÜÇGENİ ÖZELLİKLERİ Okul(8 15 17) Üçgeni (7 24 25) Üçgeni (30 60 90) Üçgeni (30 30 1) Üçgeni (15 75 90) Üçgeni (45 45 90) Üçgeni; Yukarıdakileri özetleyerek, ABQ üçgeninin SCD üçgenine eşit olduğunu ve bu nedenle, AQ = SD = (AD BC) / 2 = (a b) / 2 segmentini söylemek doğru olur 3 4 İyi tavsiye

Ucgenler Alkan Hoca Matematik Yks Tyt Ays Kpss Ales Dgs Ygs Lys Teog

Dik Ucgende Trigonometri Bikifi

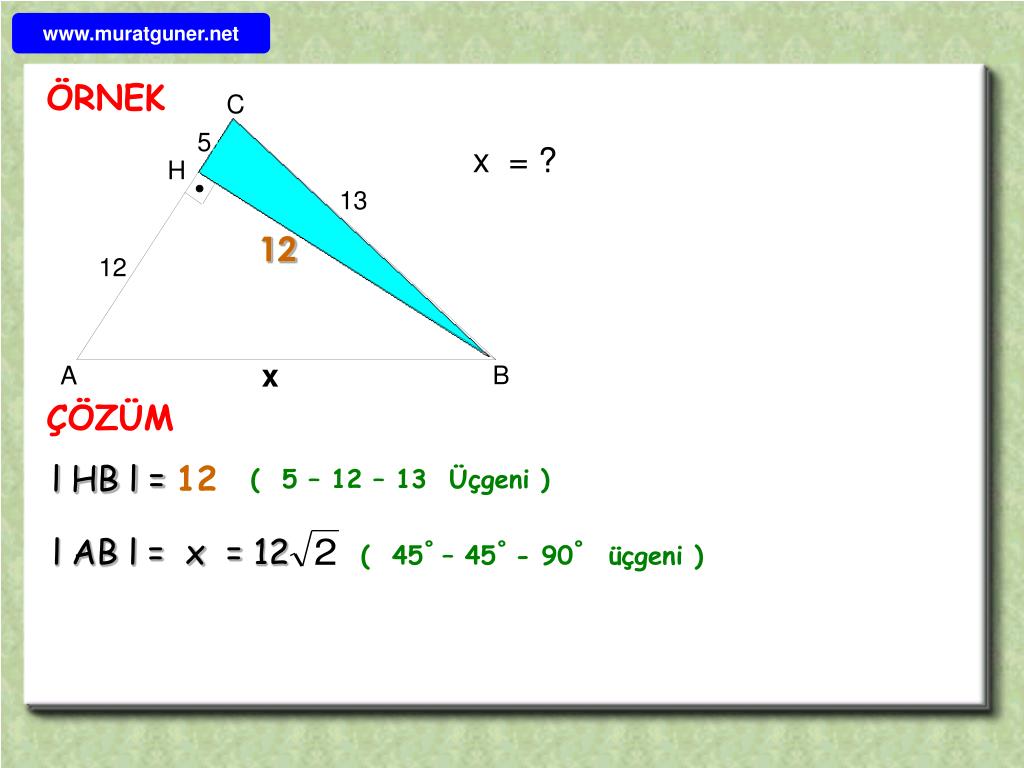
5 12 13 üçgeninin iç açıları şu şekildedir Uzunluğu 5 ile orantılı olan kenarı gören açının ölçüsü 23 derecedir Üçgen nedir ve özellikleri nelerdir? (15° 75° 90°) ABC üçgeninin alanını iki farklı şekilde yazıp eşitlediğimizde Gottfried Wilhem Leibnitz kimdir hayata gülümseme Isaac Newton hayatı ve eserleri Isaac Newton15 75 90 üçgeninde hipotenüste bulunan yükseklik indirildiği zaman iki farklı 15 75 90 üçgeninin meydana geldğini söylemek mümkündür

15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz

Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir

(30 60 90) Üçgeni (30 60 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz Sizi ve arkadaşlarınızı sitemize02Eyl17 Bu Pin, Mustafa YAZAGAN tarafından keşfedildi Kendi Pinlerinizi keşfedin ve 'e kaydedin! Kosinüs Teoremi Bir üçgende bir kenarın karesi, diğer iki kenarın kareleri toplamından, bu iki kenar ile bu kenarlar arasındaki açının kosinüsü çarpımının iki katı eksiğine

X 2x X 5 Ucgeni Tam Olarak Nedir Acaba Sorularda Nasil Kullanilir Lutfen Yardimci Olun Eodev Com

Ppt Dik Ucgende Metrik Bagintilar Powerpoint Presentation Free Download Id

 8 15 17 özel üçgeninin iç açıları nedir Bu soruya açıklama yazılmamış Dik Üçgenin Özellikleri (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait 15° 75° 90° üçgeni, Özel bir üçgendir 30° 60° 90° üçgeni ve 15° 15° 150° üçgenidir ABC üçgeninin içine çizilen HAD üçgeninde;Dr C Erdem İMRAK Dr İsmail GERDEMELİ MAK419 Transport Tekniği f 7 113 BANTLI KONVEYÖRLERİN KONSTRÜKSİYONU 1131 Bantlı Konveyörün Çalışma Prensibi Konveyör

45 45 90 Ucgeni Kurali Nedir 45 45 90 Ucgeninin Ozellikleri Nelerdir En Son Haberler

3 4 5 Ucgeni Ve Ozellikleri Not Bu

Torpilcom, uzaktan eğitim portalı olarak, 05 Kasım 16 Kasım aralığında, internet ortamında "üniversite ve lise giriş sınavlarına hazırlanan" öğrencilere, ücretsiz eğitim destek içerikleri

Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz

Ozel Ucgenler Dik Ucgen Ppt Indir

15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz

3

15 75 90 Ucgeni Ozellikleri Ve Kurallari

1

Dik Ucgen Derspresso Com Tr

Dik Ve Ozel Ucgenler

15 45 1 Ozel Ucgeni Var Mi Varsa Kurali Nedir Eodev Com

Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir

Ozel Ucgenler Konu Anlatimi

15 75 90 Ucgeni

Scalene Ucgeni Ozellikler Formul Ve Alanlar Hesaplama Bilim 22

15 75 90 Ucgeninin Ozellikleri Nelerdir

30 30 1 Ucgeni Not Bu

15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeni Alan Ve Kenar Bagintilari Konu Anlatimi

Trigonometria Foro General Rincon Matematico

Ozel Ucgenler Pdf

Ucgen Ve Cokgenlerle Ilgili Soru Ve Alistirmalar

1

2

Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt

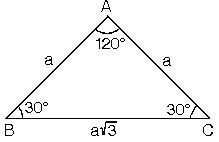
Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir

Ucgenlerde Uzunluk Matematik Ve Geometri

Dik Ucgen Derspresso Com Tr

Dik Ucgende Trigonometri Bikifi

15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim

Ph Ab Ph X Kac Cm Dir Pdf Ucretsiz Indirin

15 75 90 Ucgeni Not Bu

Dik Ucgen Derspresso Com Tr

Top 19 80 80 Ucgeni Ozelligi En Iyi 22

Net Fikir Dik Ucgen Ve Temel Ozellikleri

Dik Ucgen Derspresso Com Tr

30 60 90 Ucgeni Ozellikleri

Eskenar Ucgen

Dik Ucgen Vikipedi

45 45 90 Ucgeni Matematikce

Dik Ucgen 16 15 75 90 Ucgeni Matematik Felsefesi Temel Matematik Evde Egitim

Ucgenin Alani Neler Ogrenecegiz Baslarken Pdf Ucretsiz Indirin

Ispat 15 75 90 Ucgeni Tyt Geometri Ozel Ucgenler Youtube

15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz

Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir

15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeninin Ozellikleri Nelerdir Egitim Haberleri

Geometrik Kavramlar Geometride Nokta Dogru Duzlem Gibi Kavramlar Tanimsiz Olarak Kabul Edilir Ppt Indir

Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir

Trigonometri Dik Ucgenlerdeki Trigonometrik Oranlar Matematikciler Com

Ozel Ucgenler Konu Anlatimi

2

Net Fikir Aralik

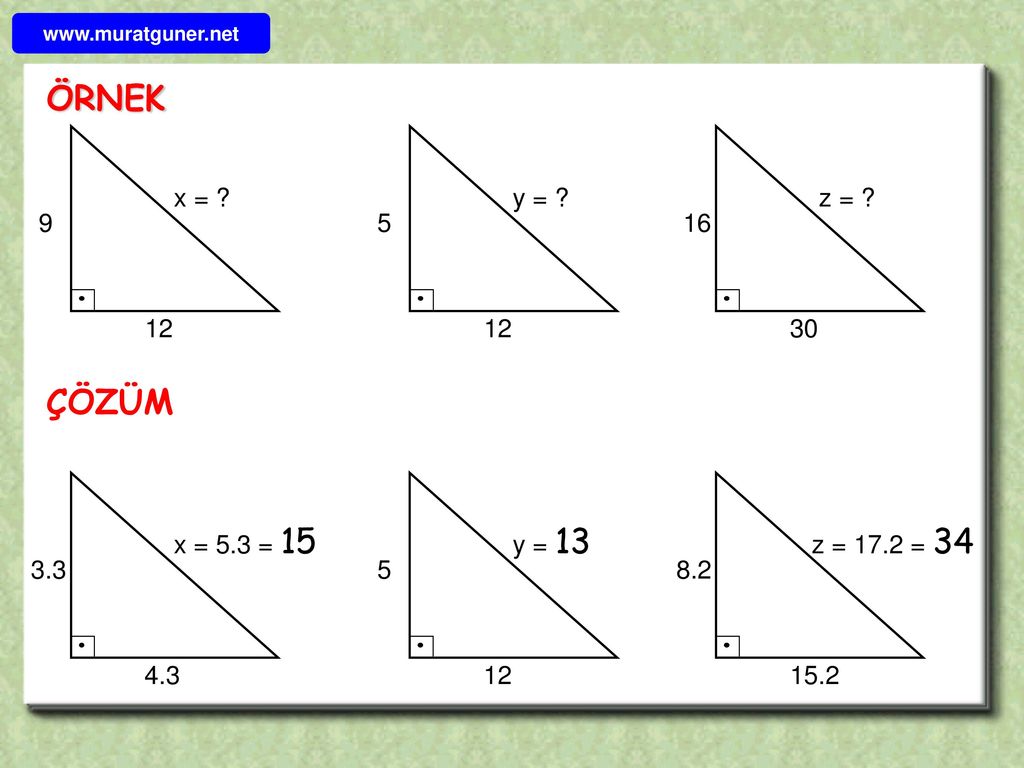
Matematik Ogrenebilir Ppt Indir

Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz

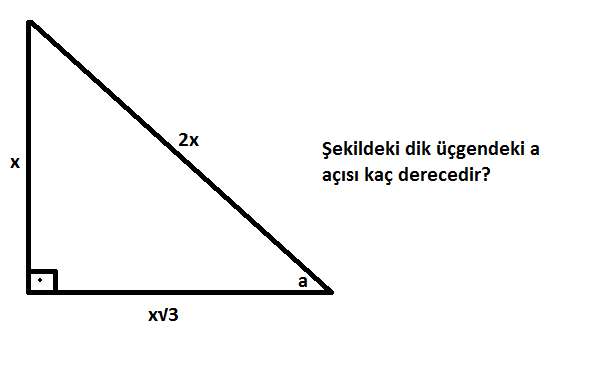
Acill Ozel Geometri Sorusu

2

Geometri 15 75 90 Ucgeni Nasil Olur Youtube

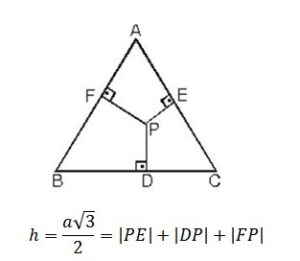
Ozel Ucgenler Konu Anlatimi

2

Dik Ucgen Derspresso Com Tr

75 15 90 Ucgeni Acilarina Gore Ozel Dik Ucgenler

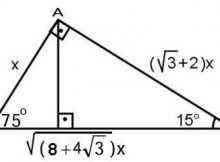
Ozel Ucgenler Not Bu

Dik Ucgende Trigonometri Bikifi

Ucgende Alan Formulleri Ve Bagintilari Matematik Ogretmenleri

22 5 67 5 90 Ucgeni Ozelligi Matematik Sarisin Renkli Okuma

Acilarina Gore Ucgenler Ppt Indir

15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube

30 60 90 Ucgeni Ve Ozellikleri Not Bu

15 75 90 Ucgeni Webders Net

15 75 90 Ucgeni Ozellikleri Ve Kurali Soru List

15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz

30 60 90 Ucgeninin Ozellikleri

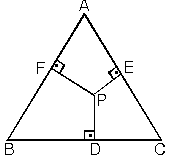
Ozel Ucgenler

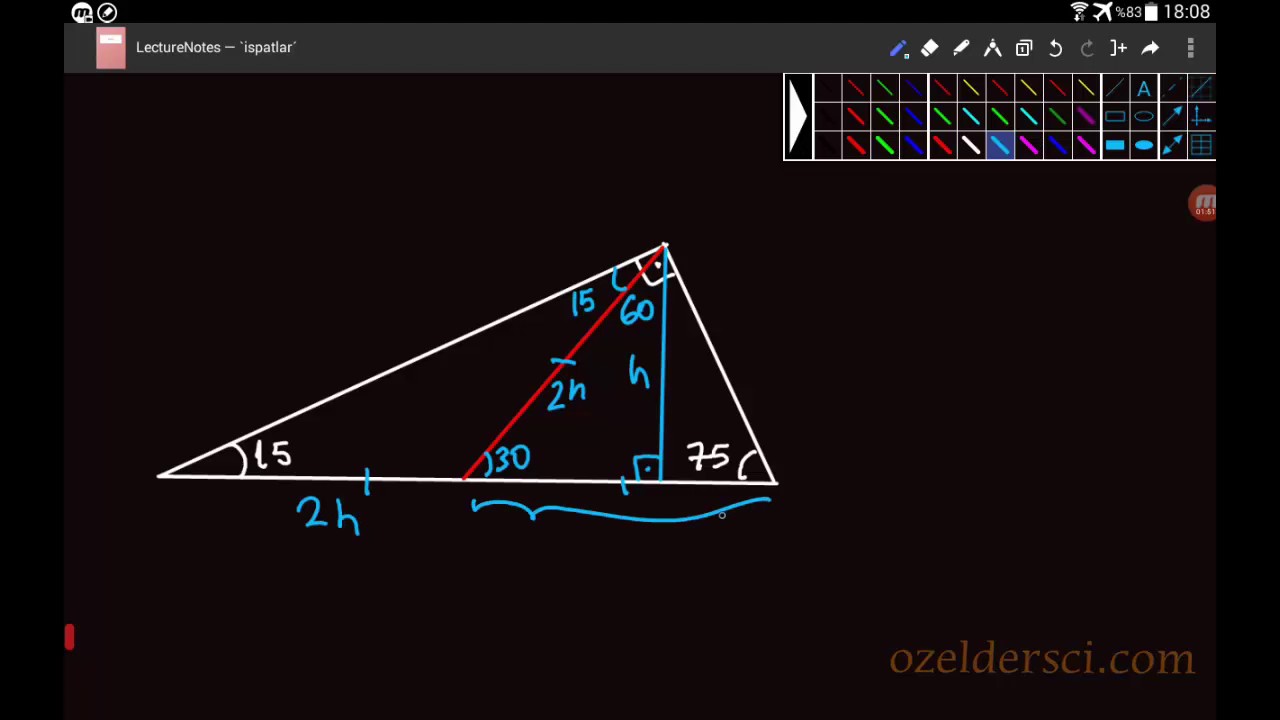
15 75 90 Ucgeni Ozelliklerinin Ispati Youtube

Murat Sen Akdeniz Universitesi Ucgenler Ppt Video Online Indir

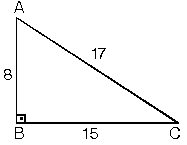
Dik Ucgen Ve Ozellikleri

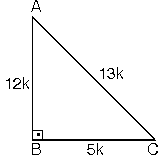
Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir